Analisis Data Statistika

ANALISIS DATA APLIKASI STATISTIKA

1. Pengertian Analisis Data

Analisis data diartikan sebagai upaya mengolah data menjadi informasi, sehingga karakteristik atau sifat-sifat data tersebut dapat dengan mudah dipahami dan bermanfaat untuk menjawab masalah-masalah yang berkaitan dengan kegiatan penelitian. Dengan demikian, teknik analisis data dapat diartikan sebagai cara melaksanakan analisis terhadap data, dengan tujuan mengolah data tersebut menjadi informasi, sehingga karakteristik atau sifat-sifat datanya dapat dengan mudah dipahami dan bermanfaat untuk menjawab masalah-masalah yang berkaitan dengan kegiatan penelitian, baik berkaitan dengan deskripsi data maupun untuk membuat induksi, atau menarik kesimpulan tentang karakteristik populasi (parameter) berdasarkan data yang diperoleh dari sampel (statistik).

2.     Tujuan Analisis Data

(a) Mendeskripsikan data, biasanya dalam bentuk frekuensi, ukuran tendensi sentral maupun ukuran dispersi, sehingga dapat dipahami karakteristik datanya. Dalam statistika, kegiatan mendeskripsikan data ini dibahas pada statistika deskriptif. (b) Membuat induksi atau menarik kesimpulan tentang karakteristik populasi, atau karakteristik populasi berdasarkan data yang diperoleh dari sampel (statistik). Kesimpulan yang diambil ini bisanya dibuat berdasarkan pendugaan (estimasi) dan pengujian hipotesis. Dalam statistika, kegiatan membuat induksi atau menarik kesimpulan tentang karakteristik populasi  atau sampel ini dibahas pada statistika inferensial.

3.     Langkah dan Prosedur Analisis Data

(a) Tahap mengumpulkan data, dilakukan melalui instrumen pengumpulan data.(b) Tahap editing, yaitu memeriksa kejelasan dan kelengkapan pengisian instrumen pengumpulan data. (c) Tahap koding, yaitu proses identifikasi dan klasifikasi dari setiap pertanyaan yang terdapat dalam instrumen pengumpulan data menurut variabel-variabel yang diteliti. (d) Tahap tabulasi data, yaitu mencatat atau entri data ke dalam tabel induk penelitian. (e) Tahap pengujian kualitas data, yaitu menguji validitas dan realiabilitas instrumen pengumpulan data. (f) Tahap mendeskripsikan data, yaitu tabel frekuensi dan/atau  diagram, serta berbagai ukuran tendensi sentral, maupun ukuran dispersi. tujuannya memahami karakteristik data sampel penelitian. (g) Tahap pengujian hipotesis, yaitu tahap pengujian terhadap proposisi-proposisi yang dibuat apakah proposisi tersebut ditolak atau diterima, serta bermakna atau tidak. Atas dasar Pengujian hipotesis inilah selanjutnya keputusan dibuat.

4.     Macam Analisis Data

Teknik analisis data dalam penelitian, dibagi menjadi dua, yaitu teknik analisis data diskriptif dan teknik analisis data inferensial. Teknik analisis data penelitian secara deskriptif dilakukan melalui statistika deskritif, yaitu statistik yang digunakan untuk menganalisis data dengan cara mendeskripsikan atau menggambarkan data yang telah terkumpul sebagaimana adanya tanpa bermaksud membuat generalisasi hasil penelitian. Temasuk dalam teknik analisis data statistik deskriptif antara lain penyajian data melalui tabel, grafik, diagram, persentase, frekuensi, perhitungan mean, median atau modus.

Sementara itu teknik analisis data inferensial dilakukan dengan statistik inferensial, yaitu statistik yang digunakan untuk menganalisis data dengan  membuat kesimpulan yang berlaku umum. Ciri analisis data inferensial adalah digunakannya rumus statistik tertentu (misalnya uji t, uji F, dan lain sebagainya). Hasil dari perhitungan rumus statistik inilah yang menjadi dasar pembuatan generalisasi dari sampel bagi populasi. Dengan demikian, statistik inferensial berfungsi untuk menggeneralisasikan hasil penelitian sampel bagi populasi. Sesuai dengan fungsi tersebut maka statistik inferensial cocok untuk penelitian sampel.

5.     Terminologi dalam Analisis Data: Metode Succesive Interval

Contoh :
Sebuah item yang memenuhi kriteria Likert dengan lima kategori respon, yaitu “sangat setuju” yang diberi skor 5; “setuju” diberi skor 4; “ragu-ragu” diberi skor 3; “tidak setuju” diberi skor 2; dan “sangat tidak setuju” diberi skor 1. Item tersebut dijawab oleh 100 orang responden. Untuk kepentingan analisis data, peneliti kemudian bermaksud menaikkan tingkat pengukuran ordinal menjadi interval.

Langkah kerja MSI:

• Perhatikan banyaknya (frekuensi) responden yang menjawab atau memberikan respon terhadap alternatif jawaban yang tersedia. Misalnya: Frekuensi yang memilih jawaban “sangat setuju” = 25 orang; frekuensi yang memilih jawaban “setuju” = 17 orang; frekuensi yang memilih jawaban “ragu-ragu” = 34 orang; frekuensi yang memilih jawaban “tidak setuju” = 19 orang; dan frekuensi yang memilih jawaban “sangat tidak setuju” = 5 orang.
• Bagi setiap bilangan pada frekuensi oleh banyaknya responden (yaitu n = 100). Berdasarkan langkah pertama diperoleh proporsi sebagai berikut:

Proporsi jawaban “Sangat Setuju” :  25/100 = 0,25
Proporsi jawaban “Setuju” : 17/100 = 0,17
Proporsi jawaban “Ragu-ragu” : 34/100 = 0,34
Proporsi jawaban “Tidak Setuju”: 19/100 =0,19
Proporsi jawaban “Sangat Tidak Setuju”  : 5/100 = 0,05
Jumlahkan proporsi secara beruntun sehingga diperoleh proporsi kumulatif (PK) berikut : 

Pk₁ = 0,25
Pk₂ = 0,25 + 0,17 = 0,42
Pk₃ = 0,42 + 0,34 = 0,76
Pk₄ = 0,76 + 0,19 = 0,95
Pk₅ = 0,95 + 0,05 = 1

• Menentukan nilai Z untuk setiap kategori. Sebelum menentukan nilai Z, perlu kita ketahui bahwa karakteristik kurva normal baku yang dikembangkan oleh Karl Gauss ini memiliki karakteristik: (a) kurvanya simetris, (b) kurvanya selalu di atas sumbu x atau berasimtut sumbu x (mendekati sumbu datar x atau memotong sumbu x pada x = ~), dan (c) luas kurva normal adalah luas antara kurva normal dengan sumbu datarnya yaitu sama dengan 1 satuan luas, yang terentang dari “min” tak terhingga (- ~) sampai dgn “plus” tak terhingga (+ ~).

Kurva Normal Baku

Perlu diperhatikan bahwa tanda “plus” dan “minus” dalam gambar selain merupakan tanda aljabar juga merupakan tanda arah. Tanda “plus” menandakan daerah kurva berada di sebalah kanan, yang dibatasi oleh garis simetris dan “plus” tak terhingga (+ ~). Sementara tanda “min” menandakan daerah kurva berada di sebelah kiri, yang dibatasi oleh garis simetris dan “min” tak terhingga (- ~). Berdasarkan keterangan di atas, terutama berkaitan dengan karakteristik kurva normal yang simetris, maka dapat diketahui bahwa luas kurva normal dari garis simetris ke “plus” tak terhingga (+ ~) adalah 0,5 satuan luas, dan luas kurva normal dari garis simetris ke “min” tak terhingga (- ~) juga sama yaitu 0,5 satuan luas, yang apabila dijumlahkan menjadi satu satuan luas.

Setelah kita membahas tentang kurva normal di atas, selanjutnya kita dapat menentukan nilai Z untuk setiap kategori pada skala Likert yaitu 5 untuk kategori “Sangat Setuju”, 4 untuk kategori “Setuju”, 3 untuk kategori “ragu-ragu”, 2 untuk kategori “Tidak Setuju”, dan 1 untuk kategori “Sangat Setuju”. Sebagai patokan untuk menentukan nilai Z setiap kategori adalah proporsi kumulatif yang diperoleh pada langkah ketiga. Sehingga nilai-nilai Z nya  adalah :

Nilai Z₁ :  0,5 – Pk₁ = 0,5 – 0,25 = 0,25 maka Z₁ adalah = -0,67
Nilai Z₂ :  0,5 – Pk₂ = 0,5 – 0,42 = 0,08 maka Z₂ = -0,20
Nilai Z₃ :  Pk₃ – 0,5 = 0,76 – 0,5 = 0,26 maka Z₃ = 0,70
Nilai Z₄ :  Pk₄ – 0,5 = 0,95 – 0,5 = 0,45 maka Z₄ = 1,64
Nilai Z₅ :  Pk₅ = 1, maka Z₅ = ~

Untuk  memahami dari mana nilai-nilai Z diperoleh, perhatikan penjelasan berikut!

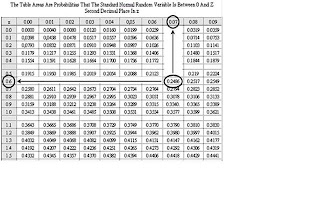
Nilai Z₁ = -0,67, diperoleh berdasarkan nilai peluang 0,25 pada Tabel Z atau Tabel Distribusi Normal Baku. Pada Tabel Z ini memuat dua hal yaitu, nilai Z dan peluangnya. Perhatikan ilustrasi berikut

Dari gambar di atas, kita bisa mengetahui nilai Z terletak pada kolom pertama atau kolom paling kiri dari tabel, dan baris pertama atau baris paling atas dari tabel. Sementara nilai peluangnya terletak mulai dari kolom kedua dan baris kedua. Dengan demikian nilai Z terdiri dari 3 dijit, dan nilai peluangnya terdiri dari 5 dijit. Sebagai contoh perhatikan angka 0,2486 yang dilingkari pada tabel. Untuk mengetahui nilai Z dari nilai peluang 0,2486 ini, langkah pertama yang harus kita lakukan melihat nilai Z yang berada di kolom paling kiri dari tabel, yang sejajar dengan angka 0,2486. Pada tabel tertera angka 0,6. Selanjutnya untuk mencari 1 dijit tersisa, langkah yang harus kita lakukan adalah melihat nilai Z yang berada di baris paling atas dari tabel, yang sejajar dengan angka 0,2486. Pada tabel tertera angka 0,07. Kedua nilai Z yang kita peroleh tadi apabila kita gabungkan (untuk mempermudah, kita bisa menjumlahkannya, yaitu 0,60 + 0,07 = 0,67) akan diperoleh angka 0,67. Dengan demikian nilai Z untuk nilai peluang 0,2486 adalah 0,67.

Kembali pada kasus yang sedang kita bahas, untuk menentukan nilai Z₁ dari nilai peluang 0,25, kita bisa melakukan langkah seperti yang telah kita bahas pada contoh. Pada kasus kita ini nilai peluang 0,25 tidak terdapat pada tabel. Apabila kita menemukan hal seperti ini, maka langkah yang dapat kita lakukan untuk mencari nilai Z nya adalah dengan Interpolasi Linier. Istilah interpolasi linier diartikan sebagai membuat perhitungan antara dua nilai yang ada, dengan menganggap sebuah lengkungan sebagai garis lurus.

Langkah kerjanya : (a) Perhatikan nilai peluang 0,25, terletak antara nilai peluang  berapa? Pada tabel tampak nilai peluang 0,25 terletak antara 0,2486 dan 0,2517. (b) Nilai Z pada peluang 0,2486 adalah 0,67, dan nilai Z pada peluang 0,2517 adalah 0,68. Sehingga nilai Z untuk nilai peluang = 0,25 adalah :

Jadi nilai Z untuk peluang 0,25 adalah 0,6745. Perlu kita perhatikan bahwa peluang 0,25 pada kurva normal ada di sebelah kiri sehingga harus kita beri tanda “min” pada nilai Z nya. Sehingga nilai Z₁ pada peluang 0,25 adalah -0,6745.

Nilai Z₂ dapat dihitung sebagai berikut:  (1) Perhatikan nilai peluang 0,08 pada tabel. Nilai ini terletak antara nilai peluang 0,0793 dan 0,0832. (2) Nilai Z pada peluang 0,0793 adalah 0,20, dan nilai Z pada peluang 0,0832 adalah 0,21. Sehingga nilai Z untuk nilai peluang = 0,08 adalah :

Jadi nilai Z untuk peluang 0,08 adalah 0,2018. Perlu kita perhatikan bahwa peluang 0,08 pada kurva normal ada di sebelah kiri sehingga harus kita beri tanda “min” pada nilai Z nya. Sehingga nilai Z₂ pada peluang 0,08 adalah -0,2018.

Nilai Z₃ dapat dihitung sebagai berikut:  (a) Perhatikan nilai peluang 0,26 pada tabel. Nilai ini terletak antara nilai peluang 0,2580 dan 0,2611. (b) Nilai Z pada peluang 0,2580 adalah 0,70, dan nilai Z pada peluang 0,2611 adalah 0,71. Sehingga nilai Z untuk nilai peluang = 0,26 adalah :

Jadi nilai Z untuk peluang 0,26 adalah 0,7065. Perlu kita perhatikan bahwa peluang 0,26 pada kurva normal ada di sebelah kanan sehingga harus kita beri tanda “plus” pada nilai Z nya. Biasanya tanda “plus” ini pada prakteknya jarang disertakan. Sehingga nilai Z₃ pada peluang 0,26 adalah 0,7065.

Nilai Z₄ dapat dihitung sebagai berikut: (a) Perhatikan nilai peluang 0,45 pada tabel. Nilai ini terletak antara nilai peluang 0,4495 dan 0,4505. (b) Nilai Z pada peluang 0,4495 adalah 1,64, dan nilai Z pada peluang 0,4505 adalah 1,65. Sehingga nilai Z untuk nilai peluang = 0,45 adalah :

Jadi nilai Z untuk peluang 0,45 adalah 1,645. Perlu kita perhatikan bahwa peluang 0,45 pada kurva normal ada di sebelah kanan sehingga harus kita beri tanda “plus” pada nilai Z nya. Sehingga nilai Z₄ pada peluang 0,45 adalah 1,645.

Selanjutnya untuk nilai Z₅ pada nilai peluang 1 adalah tak terhingga ( ~ ). Ingat salah satu karakteristik dari kurva normal adalah berasimtut/mendekati sumbu x. Dengan demikian pada luas sama dengan 1, maka x nya adalah sama dengan tak terhingga (~).

• Menghitung Nilai Skala (Scale Value).

Rumus :

aanvangelink.blogspot.com

Keterangan :

Area = Daerah kurva
Density= Tinggi kurva.
Nilai-nilai density diperoleh dari tabel ordinat distribusi normal baku.

Pada langkah ke empat kita sudah mendapatkan nilai Z₁, Z₂, Z₃, Z₄ dan Z₅. Selanjutnya berdasarkan nilai-nilai tersebut dan dengan bantuan tabel ordinat distribusi normal baku kita dapat memperoleh nilai density-nya. Untuk memudahkan pengerjaan, maka nilai-nilai Z yang telah diperoleh selanjutnya kita buat dalam 2 belakang koma, sesuai dengan 3 dijit angka yang ada dalam tabel Z. Oleh karena itu Z₁ dari 0,6745 menjadi 0,67, Z₂ dari 0,2018 menjadi 0,20, Z₃ dari 0,7065 menjadi 0,71, dan Z₄ dari 1,645 menjadi 1,64.

Dengan demikian nilai density nya diperoleh:

Density pada Z₁ = 0,67 adalah 0,3187
Density pada Z₂ = 0,20 adalah 0,3910
Density pada Z₃ = 0,71 adalah 0,3101
Density pada Z₄ = 0,64 adalah 0,1040
Density pada Z₅ = ~ adalah 0

Untuk  memahami dari mana nilai-nilai density diperoleh, perhatikan penjelasan berikut!

Untuk menentukan nilai density dari nilai Z₁ = 0,67 dapat dilakukan dengan langkah sebagai berikut: Pertama, yang harus kita lakukan adalah melihat nilai Z yang berada di kolom paling kiri dari tabel. Perhatikan, nilai Z pada tabel tertera hanya dua dijit, oleh karena itu kita hanya mengambil nilai Z₁ dua dijit yaitu 0,6. Satu dijit tersisa yaitu angka 7 kita lihat pada nilai Z yang berada pada baris pertama tabel. Pada baris tersebut kita pilih angka 0,07. Setelah kita menemukan angka 0,6 dan 0,07 pada tabel. Selanjutnya adalah pada angka 0,6 kita lihat ke sebelah kanan yang sejajar dengan angka 0,6 tadi. Kemudian dari angka 0,07 kita lihat ke bawah yang sejajar dengan angka 0,07. Kalau kita pertemukan dari angka 0,6 ke kanan dan 0,07 ke bawah maka akan bertemu pada angka 0,3187. Jadi nilai density untuk Z₁ = 0,67 adalah 0,3187. Dengan cara yang sama kita dapat menentukan nilai density dari Z₂, Z₃, Z₄ dan Z₅

Dengan demikian nilai skalanya (scale value) adalah:

• Lakukan transformasi nilai skala (transformed scale value) dengan rumus:Y = SV_i + |SV_Min|. Ingat: SV yang nilainya kecil atau harga negatif terbesar diubah menjadi sama dengan satu (=1).

Untuk SV₁ = -1,2748 maka Y = -1,2748 + 2,2748  = 1 (=Respon 1)

Nilai ini didapat karena SV terkecil setelah ditransformasi harus sama dengan 1, sehingga 1 – (-1,2748) = 2,2748. Nilai 2,2748 ini merupakan nilai interval yang kemudian dijumlahkan pada masing-masing SV untuk mendapatkan nilai hasil transformasi.

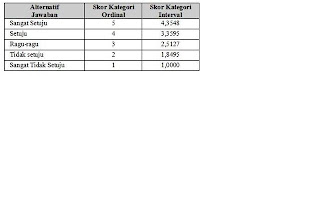
Sehingga SV hasil transformasi lainnya akan diperoleh : (a) Untuk SV₂ = -0,4253, maka Y = -0,4235 + 2,2748 = 1,8495 (= Respon 2); (b) Untuk SV₃ = 0,2379, maka Y = 0,2379 + 2,2748 = 2,5127 (= Respon 3) ; (c) Untuk SV₄ = 1,0847, maka Y = 1,0847 + 2,2748 = 3,3595 (= Respon 4); (d) Untuk SV₅ = 2,0800, maka Y = 2,0800 + 2,2748 = 4,3548 (= Respon 5).

aanvangeling.blogspot.com